Não linearidade em redes neurais com Pytorch

Dentro do contexto de redes neurais, as funções de ativação são essenciais. Uma de suas principais funções é permitir o aprendizado de regiões e superfícies de decisão mais complexas. Nesse post, iremos criar redes neurais usando Pytorch e analisar as superfícies de decisão com e sem funções de ativação.

Redes neurais

Uma rede neural é um aproximador universal de funções. O que isso quer dizer? Basicamente, uma rede neural consegue aproximar qualquer função contínua (dadas algumas condições). Quando estamos tratando de aprendizado de máquina, de modo geral, a ideia é essencialmente aproximar uma função que descreve/aprende seus dados de treino.

Dessa forma, redes neurais são ferramentas muito poderosas em problemas de classificação, em que procuramos uma superfície de decisão para conseguir dizer a qual classe um objeto pertence, e regressão, em que predizemos um valor numérico. Nesse post, iremos abordar o uso das redes em problemas de classificação.

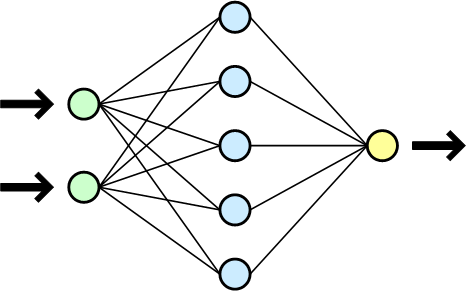
Algumas peças importantes compõem a arquitetura de uma rede neural, e os componentes básicos são: os neurônios (unidades básicas), a entrada (inputs), as camadas internas (hidden layers), as funções de ativação (activation functions) e a camada de saída (outputs). Na imagem abaixo, temos uma ilustração de uma rede:


Rede neural com uma camada de entrada, uma camada interna
e uma camada de saída. Fonte: Wikipedia

Não entraremos em detalhes sobre outros pontos igualmente relevantes no estudo de redes neurais, como funções de perda (loss functions), otimizadores (optimizers), backpropagation, etc. Em especial, iremos analisar o impacto das funções de ativação quando temos um problema de classificação com uma superfície não linear.

Exemplo em Pytorch

Um neurônio, unidade fundamental de uma rede neural, computa uma função linear do que recebe de entrada: $y = w*x + b$

Como podemos perceber, essa equação define uma reta. Em Pytorch, podemos descrever essa função como:

Se os neurônios definem retas, como uma rede pode aproximar tão bem funções complexas? Afinal, combinações de funções lineares são lineares. É ai que entra a importância das funções de ativação.

Funções de ativação

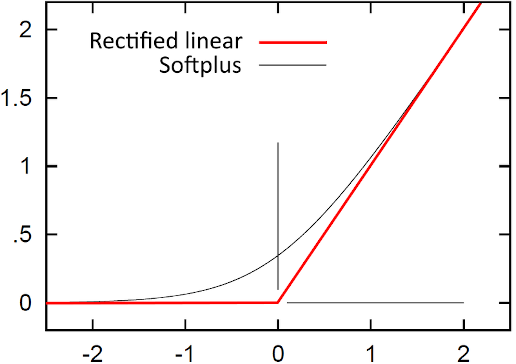
Como comentado anteriormente, um dos principais papéis das funções de ativação é adicionar não linearidade na saída de um neurônio, permitindo que a rede consiga aprender superfícies de decisão mais complexas. Existem diferentes tipos de funções de ativação, veja na figura abaixo:


Exemplo de duas funções de ativação: ReLU e Softplus. Fonte: Wikipedia

Um exemplo comum de função de ativação é a função sigmóide, descrita matematicamente como: $f(x) = \frac{1}{1+e^{-x}}$ A função sigmóide é não linear e o seu resultado são valores no intervalo entre 0 e 1. Ela, como as demais funções de ativação, introduzem o fator não linearidade na rede quando um neurônio computa: $f(y) = f(w*x + b) = \frac{1}{1+e^{-(wx+b)}}$

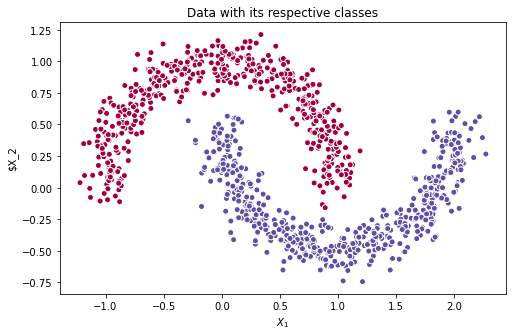
No nosso caso, o problema de classificação em questão é obtido pela função make_moons do pacote scikit-learn. Nele, temos duas features que descrevem duas classes, como na figura abaixo.


Dataset make_moons.

Iremos inicialmente montar uma pequena rede, sem nenhuma função de ativação, e verificar a superfície de decisão que ela obtêm.

Avaliando as redes no conjunto make_moons

O pacote Pytorch possui alguns módulos que auxiliam e simplificam a construção de uma rede neural. No nosso caso, iremos utilizar o módulo nn, que contém métodos e classes necessárias para a construção da rede, e o módulo optim, que contém os otimizadores para as redes.

Primeiro, é importante lembrar que o Pytorch trabalha com uma estrutura de dados chamada tensor. Um tensor seria uma generalização de um vetor em $N$ dimensões. Por exemplo, um vetor é um tensor com 1 dimensão e uma matriz é um tensor com 2 dimensões. O pacote scikit-learn, que contém a função para construirmos o conjunto de dados, utiliza vetores do numpy, e portanto, precisamos convertê-los para a estrutura torch.tensor.

Convertendo para tensor

Obtemos o conjunto de dados:

Dividimos o conjunto em treino e teste:

Convertendo para tensor:

Módulos `nn` e `optim`

O módulo nn contém componentes importantes na construção de uma rede, como o tipo das camadas, as funções de perda e ativação que iremos utilizar. Já o módulo optim contém os otimizadores para a rede.

Construindo as redes

Agora temos as peças necessárias para construir as redes que irão classificar o nosso conjunto. Assim como no pacote Keras, o Pytorch possui um módulo chamado nn.Sequential que facilita bastante a construção da rede. Também, precisamos de um otimizador, no nosso caso, Adagrad e a função de perda nn.BCELoss.

Aqui vale ressaltar que a escolha do otimizador e da função de perda não tiveram uma grande motivação, apenas que o Adagrad é um otimizador comum, e a função de perda é apropriada para classificação binária (binary cross entropy).

1° modelo

Para o primeiro modelo, com 100 unidades em uma única camada interna, temos:

Com a rede construída, precisamos treiná-la para que possa aprender as características dos dados e realizar as previsões. A função de treino:

E o loop de treino:

Resultados para o 1° modelo

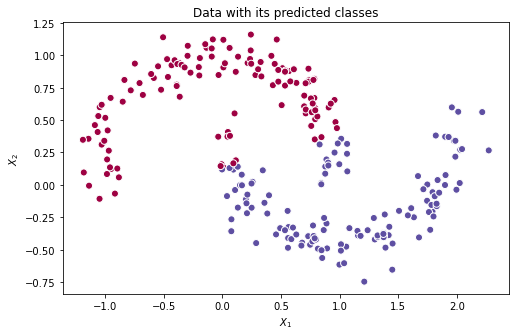
Podemos notar que o 1° modelo não contém uma função de ativação, e portanto, tem problemas em conseguir caracterizar funções mais complexas (não lineares). Um exercício interessante para analisar esse caso, é verificar a superfície de decisão:


Predições feitas pelo 1° modelo		Superfície de decisão do 1° modelo

Podemos tentar expandir essa rede (ainda sem funções de ativação) para verificar o impacto do aumento de camadas:

Obtemos os seguintes resultados:


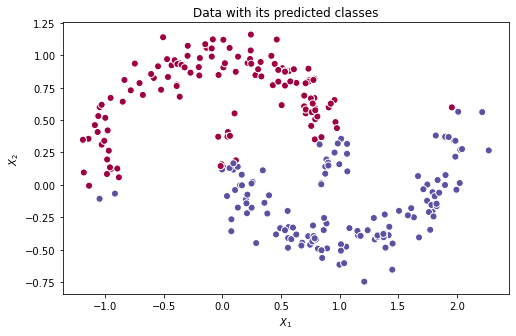
Predições feitas pelo 1° modelo com um maior número de camadas.		Superfície de decisão do 1° modelo com um maior número de camadas.

Analisando as imagens acima, fica evidente que o melhor que a rede consegue é uma reta que separa, mesmo que não perfeitamente, as duas classes (vermelha e azul), coincidindo com o que esperávamos. Pelo fato de estarmos utilizando combinações lineares, padrões não lineares são quase imperceptíveis.

2° modelo

Agora, iremos introduzir uma função de ativação no modelo, e analisar o resultado obtido. A função de ativação que iremos selecionar é a função ReLU (nn.ReLU), que matematicamente é expressa como:

\[f(x) = max(x, 0)\]

A função ReLU, por definição, é não linear (pela aplicação do máximo), e é comumente utilizada no contexto de redes neurais. Introduzindo a função de ativação, a rede terá maior capacidade de captar comportamentos não lineares nos dados.

Assim, o modelo fica:

Treinando o modelo como na etapa anterior, temos a seguinte superfície de decisão:


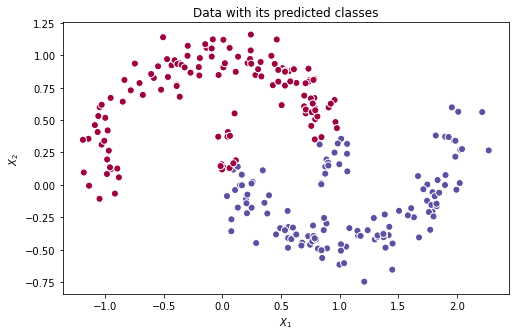
Predições feitas pelo 2° modelo.		Superfície de decisão do 2° modelo.

Podemos perceber que agora, temos uma superfície mais curvilínea, devido a introdução de não linearidade pela camada nn.ReLU. O resultado seria semelhante caso utilizássemos outra função de ativação (não necessariamente ser igual).

Construindo mais modelos

Para avaliar como as funções de ativação, atreladas a um maior número de camadas, permitem aproximarmos funções não lineares, iremos construir mais alguns modelos:

Analisando a evolução da superfície de decisão:


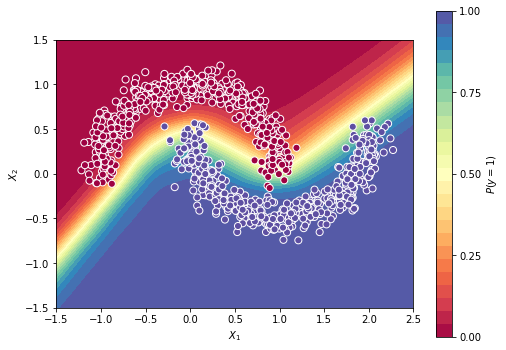
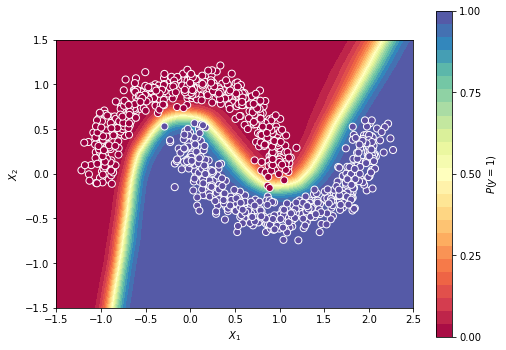
Predições feitas pelo 3° modelo.		Superfície de decisão do 4° modelo.

Fica evidente que construindo uma rede com mais camadas, atreladas a funções de ativação (não lineares), a nossa superfície de decisão consegue captar mais nuances presentes nos dados, permitindo uma classificação mais acurada. Claro, a ideia aqui é avaliar a superfície em si, já que em um contexto de uma aplicação real seria necessário avaliar também a questão da generalização da rede, que seria o quão bem a rede consegue classificar dados os quais nunca viu.

Verificamos que introduzindo as funções de ativação, junto ao aumento do número de camadas, nossa rede conseguiu captar as nuances da distribuição não linear dos dados.

Nesse post, conseguimos analisar brevemente um dos principais impactos de funções de ativação dentro do contexto de redes neurais. O tópico é uma grande área de pesquisa, com constantes novas descobertas, e apenas pincelamos o seu uso dentro do cenário de classificação.

O post também é acompanhado de um notebook, neste link.

As referências para a construção desse material foram:

Até o próximo post :)